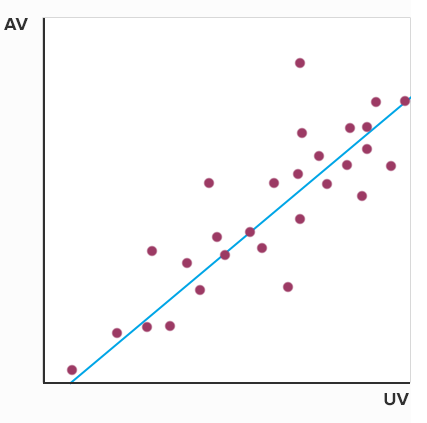
Regressionsanalyse

Eine Regressionsanalyse ist ein Modell in der Statistik, dass die Beziehung zwischen abhängigen Variablen (AV) und unabhängigen Variablen (UV) in Form einer Regressionsfunktion bzw. -geraden misst. Man unterscheidet zwischen der einfachen und der multiplen Regression und zwischen einer linearen und nichtlinearen Regression. Im Online-Marketing kann eine Regressionsanalyse eingesetzt werden, um die Kosten einer Kampagne zu analysieren und teilweise vorherzusagen.

Arten einer Regression

• Einfache Regression: Beschreibt den Zusammenhang zwischen einer unabhängigen und einer abhängigen Variable.
• Multiple Regression: Beschreibt die Korrelation multipler unabhängiger und einer abhängigen Variable.
• Lineare Regression: Zwischen unabhängigen Variablen und abhängigen Variablen besteht ein linearer Zusammenhang. Dieser lässt sich durch eine Geraden oder eine Funktion messen.
• Nicht-lineare Regression: Zwischen unabhängigen Variablen und abhängigen Variablen besteht keine lineare Korrelation. Dies ist je nach Funktions-Modell schwierig zu berechnen, da sich die Zusammenhänge nicht mit einer einfachen mathematischen Methode abbilden lassen.

Funktion einer Regressionsanalyse

In der Statistik dient ein Regressionsmodell der Analyse und der Prognose von Zusammenhängen zwischen verschiedenen Variablen und der grafischen Darstellung anhand der Messwerte. Bei dem Modell wird bei der Berechnung der Regressionsgeraden der gerichtete lineare Zusammenhang zwischen zwei (oder mehr) Variablen bestimmt. Dafür werden bestehende Daten zur Vorhersage zukünftiger Entwicklungen genutzt.

Im Online-Marketing helfen Regressionsanalysen zum Beispiel, die Daten über Conversions in der Testphase einer neuen Kampagne mit der vorherigen Conversionrate zu vergleichen.  So lässt sich beurteilen, ob sich diese erhöht hat. In dieser Regressionsanalyse wird also nach dem Zusammenhang zwischen der neuen Marketingkampagne (unabhängige Variable – UV) und der Conversionrate (abhängige Variable) gesucht. Mit anderen Worten: die einfache Regression zwischen Kampagne und Leistung der Kampagne.

Interpretation der Ergebnisse: Wichtige Kennzahlen

Das Bestimmtheitsmaß R², welches zwischen 0 und 1 liegen kann, gibt dabei an, wie gut die Regressionsgerade den Zusammenhang zwischen der UV und AV wiedergibt.

Die standardisierten Regressionskoeffizienten (Beta-Gewichte) zeigen an, welchen relativen Einfluss die unabhängigen Variablen haben. Wird bei einer multiplen Regression der Zusammenhang zwischen Alter (UV1) und Einkommen (UV2) auf den Absatz eines Produkts (AV) berechnet, kann man durch einen Vergleich der Regressionskoeffizienten feststellen, dass beispielsweise das Einkommen einen doppelt so hohen Einfluss hat, wie das Alter.

Um die Güte des Bestimmtheitsmaßes zu maximieren wird die Methode der kleinsten Quadrate angewendet. Die Methode der kleinsten Quadrate ist eine Schätzmethode, mit dessen Hilfe eine Kurve gesucht wird, die möglichst nah an den Datenpunkten der Regression verläuft. Das Bestimmtheitsmaß gibt an, wie viel Streuung durch die lineare Regressionsanalyse erklärt werden kann.

Validierung der Ergebnisse

Um zu überprüfen, ob die gefundenen Zusammenhänge signifikant sind, wird je nach Anzahl und Art der Variablen ein F- oder t-Test durchgeführt. Damit wird sichergestellt, dass die gefundene Korrelation auf die Gesamtpopulation übertragbar und nicht zufällig entstanden ist. Dabei beschreibt eine Korrelation nicht gleichzeitig eine kausale Beziehung. Zusammenhänge sind nicht gleichzeitig auch Ursache-Wirkungs-Beziehungen. Obwohl man beispielsweise einen Zusammenhang zwischen der Anzahl an Störchen und einer erhöhten Geburtenrate in einem Land findet, besteht nicht automatisch eine kausale Beziehung. Dies nennt man eine Scheinkorrelation. Logischerweise müssen andere Variablen, als die Anzahl der Störche, der Grund für die vielen Geburten sein; zum Beispiel die Größe eines Landes. Solche Effekte gilt es auch im Online-Marketing zu berücksichtigen.

Beispiel

Durch die Analyse bestehender Beziehungen zwischen unabhängigen und abhängigen Variablen, wird aufgezeigt, welchen Einfluss beispielsweise das Budget einer Facebook-Kampagne (UV) auf die Reichweite (AV) hat. Gleichzeitig lässt sich durch die lineare Regression teilweise vorhersagen, welchen Einfluss eine Steigerung oder Senkung des Budgets auf die Reichweite hätte. Ziel ist es, durch die Veränderung der unabhängigen Variablen den Einfluss auf die abhängige Variable vorherzusagen. Dies lässt sich mit sogenannten Was-wäre-wenn-Szenarien vergleichen.

Ein wichtiger Aspekt der Aussagekraft einer Regressionsanalyse ist deren Vollständigkeit. Wird eine unabhängige Variable eines Zusammenhangs außer Acht gelassen, kann das Ergebnis zwar korrekt sein, es spiegelt aber nicht die Wirklichkeit wider. Im obigen Beispiel des Einflusses des Budgets (UV1) einer Facebook-Kampagne auf deren Reichweite (AV), ist beispielsweise die Konfiguration der Zielgruppe (UV2) eine weitere unabhängige Variable, die Einfluss auf Reichweite (AV) hat. Auch die Bekanntheit der Firma oder des Produkts, die zum Beispiel durch die bestehenden Follower (UV3) gemessen werden könnte, kann einen Einfluss auf die Reichweite einer Anzeige haben. Werden nicht alle unabhängigen Variablen miteinbezogen, könnten die realen Zusammenhänge nicht korrekt aufgedeckt werden. Bei der multiplen Regressionsanalyse können diese weiteren Variablen berücksichtigt werden.

Weitere Bedeutung im Marketing

Auch lassen sich anhand von Webanalyse-Daten Kundenreisen besser verstehen. Zwar sind Regressionsanalysen aufwendig, können aber im Online-Marketing Bereich einen deutlichen Nutzen haben. Bei der Überprüfung verschiedener Werbekanäle wie Social Media, Display, E-Mail, Affiliate und Suchmaschinenwerbung, können Regressionsanalysen aufzeigen, welche Kanäle ein gutes Kosten-Nutzen-Verhältnis haben. Mit Hilfe der Ergebnisse der Analyse können in zukünftigen Kampagnen Strategien verbessert und Umsätze gesteigert werden.

Häufige Fragen

Was ist eine Regressionsanalyse?

Mit einer Regressionsanalyse kann die Beziehung zwischen einer abhängigen und einer unabhängigen Variable ermittelt werden. Sie wird häufig im Online-Marketing für eine Analyse der Kosten eingesetzt.

Welche Arten der Regressionsanalyse gibt es?

Grundsätzlich wird zwischen einer einfachen und einer multiplen sowie einer linearen und nicht-linearen Regression unterschieden.

Welche Bedeutung hat diese Analyse im Online-Marketing?

Mittels Regressionsanalysen lassen sich aufschlussreiche Erkenntnisse hinsichtlich der Customer Journey gewinnen. So kann beispielsweise das Kosten-Nutzen-Verhältnis von verschiedenen Werbekanälen ermittelt werden.

Quellen

https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/
http://www.wirtschaftslexikon24.com/d/regressionsanalyse/regressionsanalyse.htm
https://www.onlinesolutionsgroup.de/blog/glossar/r/regressionsanalyse/
https://de.ryte.com/wiki/Regressionsanalyse